
eFatigue gives you everything you need to perform state-of-the-art fatigue analysis over the web. Click here to learn more about eFatigue.
応力による疲労寿命解析(応力-寿命手法)の技術背景
応力による疲労寿命の評価法(応力-寿命手法)は,古典的な金属疲労の解析手法であり,その起源は1850年にWöhlerによって発表されています. 構造物および機械部品における応力は,材料本来の疲労限度から導かれます. この方法は,破壊に至るまでの小さな試験片を用いた疲労試験によって得られた材料のS-N線図に基づいています.
材料特性
歴史的に見て,疲労試験は回転曲げ疲労試験法で行なわれてきました. 今日では,引張・圧縮による軸方向疲労試験データで行われることが多く,この方法が一般的です.
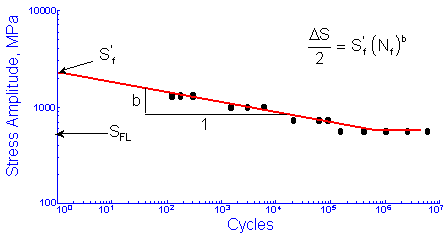
疲労限度SFLは,実験室レベルの疲労試験において材料が疲労破壊が発生しない応力です. Wöhlerは,これを設計のための安全応力レベルと呼びました. 今日我々は,これまでの疲労試験で使用される106から107回の繰返し数よりも長い超長寿命領域において,安全応力レベル(疲労限度)以下でも材料が疲労破壊することを知っています. S-N線図の有限寿命部分は,応力振幅ΔS/2と疲労寿命Nfを関連づける関数を得る場合に必要です. ここで,ある研究者は疲労データをプロットする際に,反転数2Nfを用いていることに注意してください.1回の繰返し当りに2回の反転数があります. 1回の繰返し数における切片Sfと勾配bは,材料定数として与えられます.
多くの材料の疲労特性はあまり知られておらず,引張特性から評価しなければなりません.疲労強度と引張強度は強い相関があります.
(From Forrest, Fatigue of Metals, Pergamon Press, London, 1962)
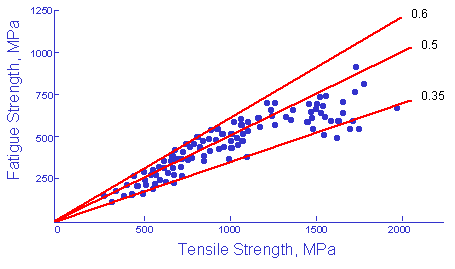
疲労限度は、およそ引張強度の2分の1になります.
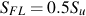
多くの合金鋼は,熱処理や焼入れが可能であり,既知の引張強度より高くなっています. 上図に示すように,疲労強度と引張強度の関係は大きくばらつきますので,熱処理などを施している場合は,表面の状態を表すブリネル硬さから疲労強度を推定することが有効です. なお,引張強度はブリネル硬さBHNのおよそ半分になることはよく知られています. このように,ブリネル硬さBHNと引張強度の両方を組み合わせることで,熱処理材の疲労強度を評価することも可能です.
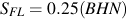
1000回程度の繰返し数における疲労強度が,約0.9 Suになることはこれまでに知られています. これは,S-N線図を求める際に,硬さからS-N線図上の2つの点を導くことが可能であることを表しています.
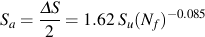
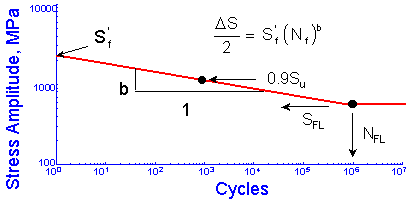
Sf',b,SFLおよびNFLの4つの材料パラメータは,材料のS-N線図を描くために必要です. なお,この4つのパラメータの内,3つのパラメータは独立です.パラメータ欄のうちの1つを残した場合には,4番目の値が算出されます. 4つすべて値が入力された場合には,SFLの値が無視されます.
修正係数
実験室レベルの材料試験で使用される材料は,実際に使用される材料の条件(表面粗さ、残留応力など)とはほとんどの場合で異なっています. 解析において重要な事項は,対象とする機械部品や機械構造物の材料の疲労強度を評価するために,それに応じて基本的な材料特性データを修正することです. 表面状態が機械部品の疲労強度に大きな役割を果たすように,疲労き裂はたいてい表面から発生します. 実験室レベルの材料試験で使用される試験片は,表面粗さの影響を無くすために表面を電解研磨等の処理が施されます. 表面損傷の度合いは,加工ばかりでなく材料強度にも依存します.高強度材料の場合には,特に表面損傷に敏感です. 解析において表面状態を考慮すると,材料の疲労強度は基礎データの疲労強度から表面仕上係数KSFだけ減少することになります.
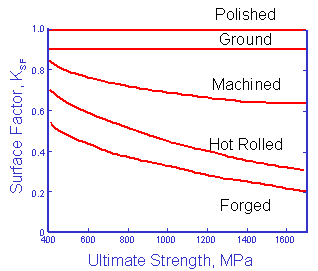
このグラフを作成するためのオリジナルのデータを下図に示しています.表面仕上係数は,疲労寿命に低下させる傾向があります.
(From Noll and Lipson, "Allowable Working Stresses", Society for Experimental Stress Analysis, Vol. III, no. 2, 1949)
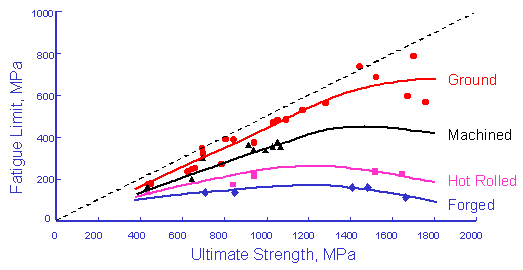
これらのデータは,様々な硬さの鋼の表面係数の評価を得るために,べき乗関数として表されます.
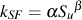
| α | β | |
| 研削 | 1.58 | -0.085 |
| 切削 | 4.51 | -0.265 |
| 熱間圧延 | 57.7 | -0.718 |
| 鍛造 | 272 | -0.995 |
これまでの疲労限度の多くは,直径6mm程度の小さな試験片を用いて回転曲げ疲労試験によって求められてきました. 引張・圧縮疲労試験によって求められた高強度材料では,より短い疲労寿命を有する傾向にあります. 経験的な荷重形態係数KLは,参照する疲労限度データと疲労限度を求める状態で負荷形式が異なる場合に用いられます.
| kL | |
| 引張・圧縮, Su <= 1500 MPa | 0.92 |
| 引張・圧縮, Su > 1500 MPa | 1.0 |
| 曲げ | 1.0 |
| ねじり | 0.58 |
これまでの研究で,小さな機械部品は大きな機械部品よりも高い疲労強度を持つことが分かっています. これは,寸法効果と呼ばれ,寸法効果係数(勾配係数)Ksizeを導入することによって疲労解析で考慮することができます. ほとんどの場合,丸棒の直径に基づいて考慮されます.
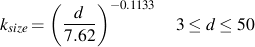
このシンプルな近似における問題の1つは,断面が丸でない場合です. この問題は,有効直径を定義することで解決されます. 任意断面形状において最大応力の95%にさらされる材料の体積が,同じ大きさの応力を受ける体積を持つ丸棒に等しくなるように求めます. これらの体積が均等になるとき,長さは無視されて比率は相対面積の一つになります. もし,最大応力の95%以上にさらされる非円形断面の断面積をA0.95として定義すれば,次式によって有効直径を与ることができます.
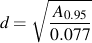
以上,これらの修正係数が決定されれば,それが使用される機械部品の疲労限度は,標準試験片の結果から下式で見積もることができます.
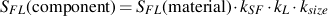
鉄鋼材料に適用したとき、これらの一般化された経験的な係数は大きな信頼性を有します. なぜなら,それらは100年以上の疲労試験で蓄積された鉄鋼材料の広範囲なデータベースに由来するものだからです. なお,それぞれの係数は近似するためのものであり,疲労試験の結果はかなり大きくばらつきます. したがって,実際の使用状態を再現した疲労試験結果の代用にしてはいけません. すなわち,公表されたデータがない場合の最初の近似データとして用いるべきということです.
応力集中
応力集中は、さまざまな機械構造物や機械部品の疲労寿命に影響を及ぼす最も重要因子の1つです. このような応力集中の発生は,あるとき設計段階で故意に与えているものかもしれませんし,あるいは深い切欠きやの加工欠陥のように,偶発的なものかもしれません. このような機械部品において,評価された疲労強度と応力集中による最大応力を直接比較することは,ある意味合理的に見えます.
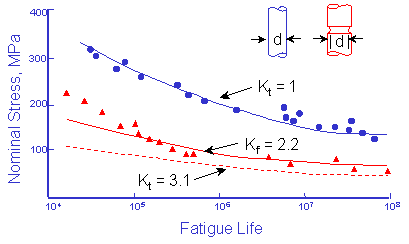
(From MacGregor and Grossman, "Effects of Cyclic Loading on Mechanical Behavior of 24S-T4 and 75S-T6 Aluminum Alloys and SAE 4130 Steel", NACA TN 2812, 1952)
上図において,青丸でプロットされた結果は,グラフの右上に青色で描いた平滑試験片の試験結果です. この幾何学形状は応力集中係数Kt=1です.赤色の破線は,図中の赤線で描かれた切欠きを持つ試験片の応力集中係数Kt=3.1で見積もられたデータを示します. 赤い三角で示された実際の疲労試験データ,赤線で示した見積もったグラフよりも高くなっていることがわかります. また,この実際の疲労試験データの応力集中係数を求めてみると,Kt=2.2となり,実際の応力集中係数Kt=3.1よりも小さくなっています. この実際に有効な応力集中係数は,金属疲労の分野では「切欠き係数Kf」と呼ばれます. Kf と Kt の違いは,材料自体の強度と切欠きの大きさに依存します. 切欠きに対して敏感な材料は,Kf = Ktとなりますが,切欠きに鈍感な材料の場合には,Kfは1に近づいていきます. 材料の切欠き敏感性 q は,この敏感性を定量化するために用います.
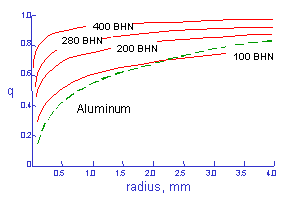
(From Peterson "Notch Sensitivity", Metal Fatigue, Sines and Waisman, McGraw Hill, 1959)
切欠き底半径が小さい場合,切欠き半径が大きい場合に比べて,疲労特性に対してあまり影響を及ぼしません. 切欠き係数 Kf は,Kt と q から次式で計算することができます.
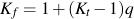
ピーターソンは,引張強さSuおよび切欠き半径 ρ in mm を用いてKfを求めるために,鋼とアルミニウムの試験結果と比較しています.
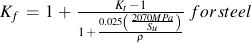
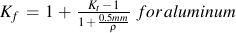
塑性変形は,より短い寿命において応力集中の影響を弱めます.切欠き係数は,寿命がより短くなるとともに小さくなります. 延性材料における応力集中は,構造物の全体的な強さを決定する場合において大きく影響しません. この特性は,静的な引張試験が機械部品の疲労特性に関する情報をほとんど与えなくなるという面も持っています. 切欠きをもつ機械部品のS-N線図の評価は,下図に示すように,平滑試験片の繰返し数1回の応力(すなわち,引張強度)から106回における疲労限度まで直線を描いたときの差がKfであり,様々な修正係数を含んでいます.
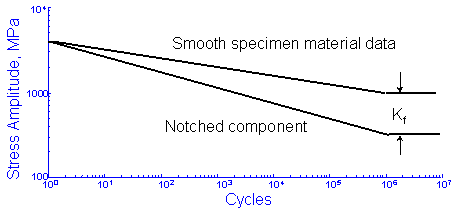
上図のように,切片は変わらずに材料のS-N線図の勾配だけが変化します.もし修正係数が含まれる場合,この新しい勾配 bnotch は下式として計算することができます.
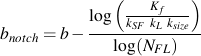
上式から,新たな切欠き材のSN線図は下式で与えられます.
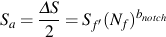
平均応力
引張の平均応力は,機械部品の疲労強度を低下させることはすでに知られています. 逆に圧縮の平均応力は,疲労強度を向上させ,加工部分の疲労強度を増加するためにしばしば用いられます. 平均応力の説明をする場合に最も一般的なのは,グッドマン線図を用いることです. グッドマン線図は1890年に最初に提案され,その中でグッドマンは「.. この理論の仮定が正当と認められるかどうかに関係なく,これが単に使いやすいものであって,事実上は Wöhlers のデータを代表するものであるから,我々はこれを採用します.」と書いています. グッドマン線図は,平均応力が0の場合の疲労強度を縦軸上にプロットされ,引張強度が横軸上にプロットされて,2つの点を直線で結ぶことで描かれます.
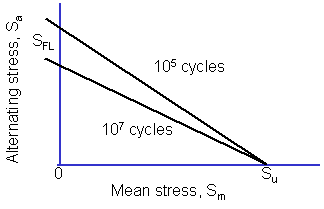
グッドマン線図は下式によって描くことができます.
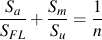
応力集中係数は,直接的にグッドマン線図に考慮することができます.
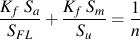
有限寿命評価においては,等価完全反転応力 Seq が計算され,機械部品のS-N線図と比較されます.
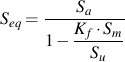
ここで Kf は,応力集中の影響がすでに機械部品のS-N線図に含まれているので,応力振幅でなく平均応力を修正するために用いられます.
上式の直接の使用は,短疲労寿命領域もしくは高平均応力状況下において問題を生じます. この問題は,実際の応力よりも弾性応力が高く計算されることによって起こります.これは,あらかじめ締付けられたボルト等が良い例です. この問題を克服する一般的な方法は,応力集中係数を平均応力ではなく応力振幅のみに適用することです. これは,適度な平均応力を備えた長寿命において,革新的な新しい評価を導く可能性を持っています. 塑性変形は,応力集中部周囲の応力を材料の引張強度と降伏応力の間の値にします. より合理的な方法は,応力集中係数を平均応力と応力振幅の両方へ適用し,その後,応力が材料の降伏応力を超えた場合に,最大応力Kf( Sa + Sm )を修正することです. 最大応力は,引張応力の約80%以下にするべきです.
 English
English